Describe the Characteristics of a Normal Distribution Using an Example

By Ra_Amber343 11 May, 2022 Post a Comment

It is symmetric unimodal ie one mode and asymptotic. The eight characteristics of a normal distribution are.

Normal Distribution Examples Formulas Uses

What are the characteristics of standard normal distribution.

. 2 It has one mode and is termed unimodal. Up to 10 cash back In a normal distribution the number of values within one positive standard deviation of the mean is equal to the number of values within one negative standard deviation of the mean. In the standard normal distribution the mean and standard deviation are always fixed.

The mean median and mode are all equal. One of the most noticeable characteristics of a normal distribution is its shape and perfect symmetry. The mean median and mode of a normal distribution are equal.

The values of mean median and mode are all equal. That means the left side of the center of the peak is a mirror image of the right side. The mean can equal any value.

The area under the normal curve is equal to 10. The normal distribution has several characteristics that make it very useful Symmetric around the mean. B Mean and median are the same.

If x 1 and x 2 are independent random variables and x 1 has normal distribution N μ 1 σ 1 and x 2 has normal distribution N μ 2 σ 2 then x 1 x 2 has normal distribution N μ 1 μ 2 σ where. 3 The area covered by the x-axis and the curve is 1. 1 It is symmetric around the point x which is equal to the mean simultaneously the mean median and mode of the distribution.

Normal distributions are symmetric around their mean. The essential characteristics of a normal distribution are. Mean median mode are equal.

The reason for this is that the values below the population mean exactly parallel the values above the mean. However a normal distribution can take on any value as its mean and standard deviation. A normal distribution is quite symmetrical about its center.

E All of the above. The number of people taller and shorter than the average height people is almost equal and a very small number of people are either extremely tall or. For example the Students t Cauchy and logistic distributions are symmetric.

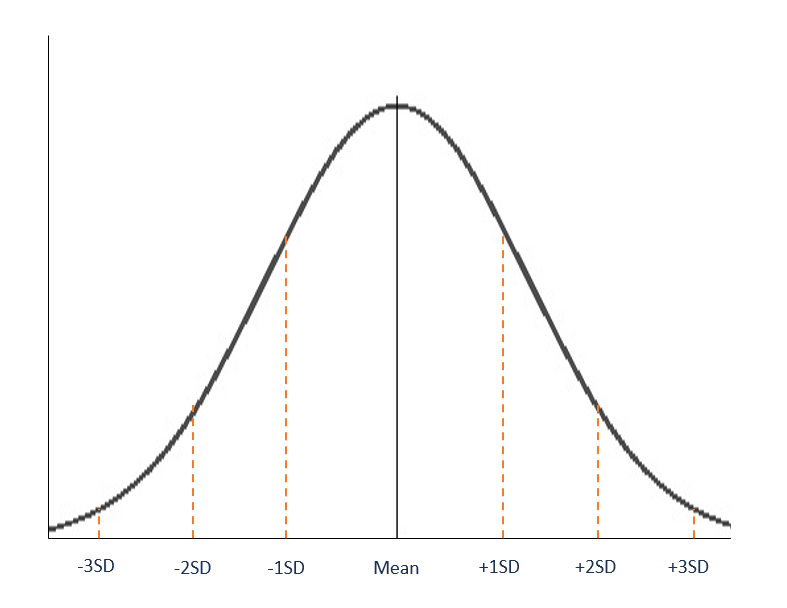
P µ - 3σ X µ 3σ 099. The normal distribution is mathematically defined. Normal distribution is theoretical.

Less common values are farther from it. Formula y 1 2 π e x μ 2 2 σ Where μ Mean σ Standard Deviation π 314159 e 271828 Example Problem Statement. A normal distribution comes with a perfectly symmetrical shape.

What are properties of the normal distribution. The precise shape can vary according to the distribution of the population but the peak is always in the middle and the curve is always symmetrical. Most of the people in a specific population are of average height.

The normal distribution is a continuous probability distribution that is symmetrical on both sides of the mean so the right side of the center is a mirror image of the left side. D Standard deviation marks the distance from the mean to the inflection point. Normal distributions are denser in the center and less dense in the tails.

C Most common values are near the mean. If you fold a picture of a normal distribution exactly in the middle youll come up with two equal halves each a mirror image of the other. In a normal distribution the mean mode and median are all the same.

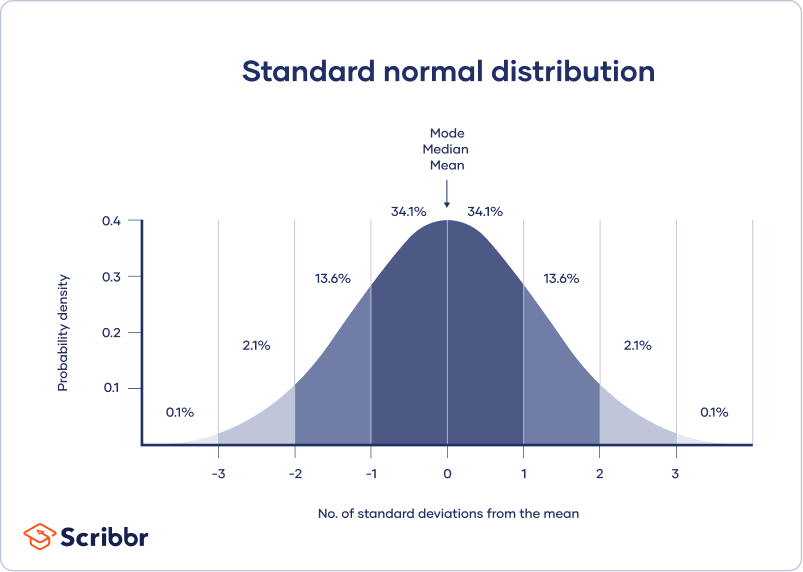
Exactly 12 of all the values are known to be to the left of centre whereas exactly half of all the values are to the right of the centre. In a normal distribution half the data will be above the mean and half will be below the mean. For example if SAT scores are normally distributed with a mean score of 550 and a standard deviation of 80 points we could generalize that 997 of SAT scores are between 550 - 3 80 310 and.

The mean median and mode are equal. While the normal distribution is symmetrical not all symmetrical distributions are normal. Statistics and Probability questions and answers.

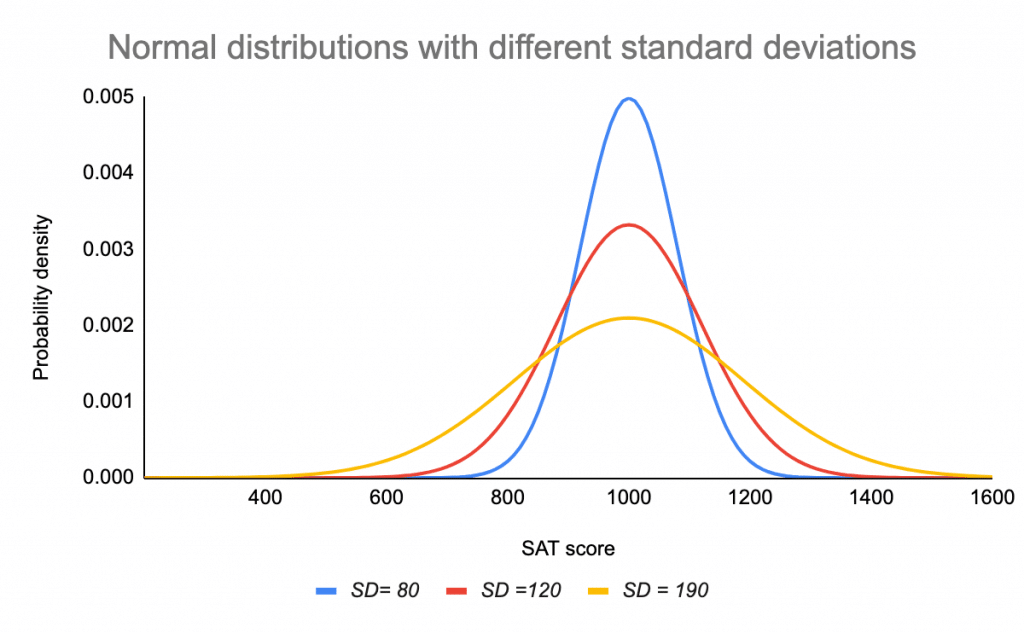
Approximately 99 of values in the distribution are within 3 SD of the mean. This means that the distribution curve can be divided in the middle to produce two equal halves. 6895997 well get back to this A normal distribution can be described with just two parameters mean and standard deviation.

If x has normal distribution Nμσ then the linear transform y ax b where a and b are constants has normal distribution Naμb aσ. The curve is known to be symmetric at the centre which is around the mean. Area under the curve 1.

What are the eight characteristics of a normal distribution. As with any probability distribution the normal distribution describes how the values of a. The area under the normal distribution curve represents.

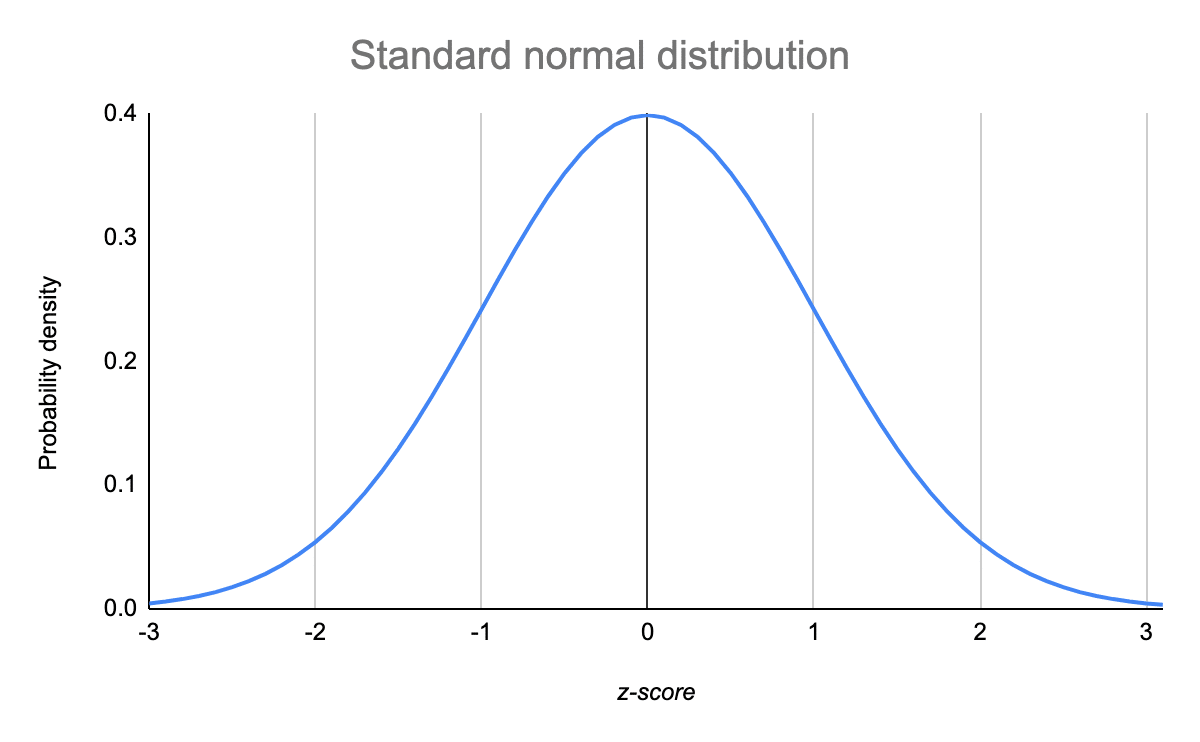
Standard deviation can equal any positive value. Using an example discuss what are the advantages if we transform a normal distribution to a standard normal distribution. All normal distributions like the standard normal distribution are unimodal and symmetrically distributed with a bell-shaped curve.

The properties of the normal distribution possessing mean as 𝞵 and standard deviation greater than 0 are as follows. The key properties of a normal distribution are listed below. The mea median mode are all located at the 50th percentile.

Describing a Normal Distribution. What are the characteristics of a normal distribution. The symmetric shape occurs when one-half of the observations fall on each side of the curve.

Height of the population is the example of normal distribution. Normal distribution is symmetrical. All of the above.

Examples of normal distributions include standardized test scores peoples heights IQ. There are many variables that are normally distributed and can be modeled based on the mean and standard deviation.

Normal Distribution Examples Formulas Uses